Notación Científica

¿Qué es la notación científica?

La notación científica es una manera rápida de representar un número utilizando potencias de base diez. 
Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.

Es usada cotidianamente en áreas como la Física y la Química , donde se usan números con varias cifras , de ahí su nombre notación científica.

Por ejemplo : 
Tenemos la siguiente cantidad 

139000000000 cm.

Ahora lo llevamos a la mínima expresión y tenemos como respuesta:

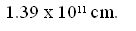
¿Cómo lo llevamos a la mínima expresión?

1. Primero, empezaremos a contar los espacios que separan a cada número de derecha a izquierda, hasta llegar al último número entero.
2. Antes de llegar a dicho número, separamos la cantidad con un punto dejando como compañía dos decimales más, (en éste caso 3 y 9).
3. Por último, multiplicamos la cantidad (1.39) por 10 (que es la base) y lo elevamos a la potencia 11 (Ya que son 11 espacios que separan a cada número).

Un video corto que lo explica mejor : 

Redondeo y Truncamiento

Los números con cifras decimales se pueden simplificar, reduciendo el número de cifras decimales lo que facilita su manejo.

Hay diversos procedimientos para realizar esta aproximación, aquí vamos a analizar el redondeo y el truncamiento. 

REDONDEOS:

Los números decimales se pueden redondear:

A la unidad: consiste en eliminar la parte decimal, aproximándola a la unidad más cercana. Si la parte decimal es igual o inferior a 0,500 se aproxima a la unidad inferior, si es superior se aproxima a la unidad superior. 
Por ejemplo: 
4,14 se aproxima a 4 (ya que la parte decimal es 0,1)
4,673 se aproxima a 5 (ya que la parte decimal es 0,6)
4,449 se aproxima a 4 (ya que la parte decimal es 0,4)

A la décima: consiste en dejar una sola cifra decimal, aproximando las centésimas a la décima más cercana. Si la parte centesimal es igual o inferior a 0,050 se aproxima a la décima inferior, si es superior se aproxima a la décima superior.
Por ejemplo:
4,449 se aproxima a 4,4 (ya que la parte centesimal es 0,04)
4,399 se aproxima a 4,4 (ya que la parte centesimal es 0,09)
4,723 se aproxima a 4,7 (ya que la parte centesimal es 0,02)

A la centésima: consiste en dejar tan sólo dos cifras decimales, aproximando las milésimas a la centésima más cercana. Si la parte milesimal es igual o inferior a 0,005 se aproxima a la centésima inferior, si es superior se aproxima a la centésima superior.
Por ejemplo:
4,673 se aproxima a 4,67 (ya que la parte milesimal es 0,003)
4,449 se aproxima a 4,45 (ya que la parte milesimal es 0,009)
4,399 se aproxima a 4,40 (ya que la parte milesimal es 0,009)

TRUNCAMIENTO:

 Truncamiento por la unidad: se eliminan todas las cifras decimales.
Por ejemplo:
45,325 se trunca por 45
122,3434 se trunca por 122
91,435123 se trunca por 91

  Truncamiento por la décima: tan sólo se deja esta cifra decimal:
Por ejemplo:
45,325 se trunca por 45,3
122,3434 se trunca por 122,3
91,435123 se trunca por 91,4

 Truncamiento por la centésima: tan sólo se dejan dos cifras decimales:
Por ejemplo:
 45,325 se trunca por 45,32
122,3434 se trunca por 122,34
91,435123 se trunca por 91,43

Volumen

Ya vimos como se calcula el área y el perímetro de las figuras, pero ahora veremos cómo se calcula el volumen de los cuerpos geométricos, pero antes, hay que saber...

¿Qué son los cuerpos geométricos?

Un Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia tiene un volumen.

Y se clasifican en:

Poliedros: Cuerpos cuyas caras son todas polígonos figuras geométricas planas.

O Redondos: Son cuerpos compuestos total o parcialmente por figuras geométricas curvas.

Estos pueden ser...
Concávo:En un poliedro cóncavo una recta puede cortar su superficie en más de dos puntos, por lo que posee algún ángulo diedro entrante. 

O Convexo:

El volumen de los cuerpos se calcula de la siguiente manera: